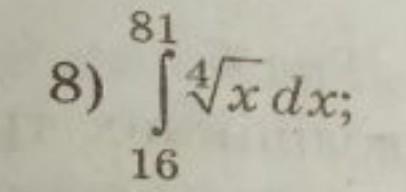Обчисліть інтеграл фотографія прикріплена ​

Ответ:

Определённый интеграл вычисляем по формуле Ньютона-Лейбница .

[tex]\bf \displaystyle \int\limits^{81}_{16}\, \sqrt[4]{x}\, dx=\int\limits^{81}_{16}\, x^{\frac{1}{4}}\, dx=\frac{4\, x^{\frac{5}{4}}}{5}\, \Big|_{16}^{81}=\frac{4}{5}\cdot \Big(81^{\frac{5}{4}}-16^{\frac{5}{4}}\Big)=\\\\\\=\frac{4}{5}\cdot \Big(\sqrt[4]{\bf 81^5}-\sqrt[4]{\bf 16^5}\Big)=\frac{4}{5}\cdot \Big(\sqrt[4]{\bf 3^{20}}-\sqrt[4]{\bf 2^{20}}\Big)=\frac{4}{5}\cdot \Big(3^5-2^5\Big)=\\\\\\=\frac{4}{5}\cdot \Big(243-32\Big)=\frac{4}{5}\cdot 211=168,8[/tex]