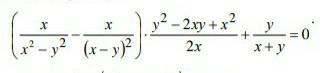довести тотожність СРОЧНО!!!​

Ответ:

Доказать тождество .

[tex]\displaystyle \bf \Big(\frac{x}{x^2-y^2}-\frac{x}{(x-y)^2}\Big)\cdot \frac{y^2-2xy+x^2}{2x}+\frac{y}{x+y}=0\\\\\\\\\Big(\frac{x}{x^2-y^2}-\frac{x}{(x-y)^2}\Big)\cdot \frac{y^2-2xy+x^2}{2x}+\frac{y}{x+y}=\\\\\\=\Big(\frac{x}{(x-y)(x+y)}-\frac{x}{(x-y)^2}\Big)\cdot \frac{(x-y)^2}{2x}+\frac{y}{x+y}=\\\\\\=\frac{x(x-y)-x(x+y)}{(x-y)^2(x+y)}\cdot \frac{(x-y)^2}{2x}+\frac{y}{x+y}=\\\\\\=\frac{x^2-xy-x^2-xy}{x+y}\cdot \frac{1}{2x}+\frac{y}{x+y}=[/tex]  

[tex]\bf \displaystyle =\frac{-2xy}{x+y}\cdot \frac{1}{2x}+\frac{y}{x+y}=\frac{-y}{x+y}+\frac{y}{x+y}=\frac{-y+y}{x+y}=\frac{0}{x+y}=0\\\\\\0=0[/tex]  

Тождество доказано .