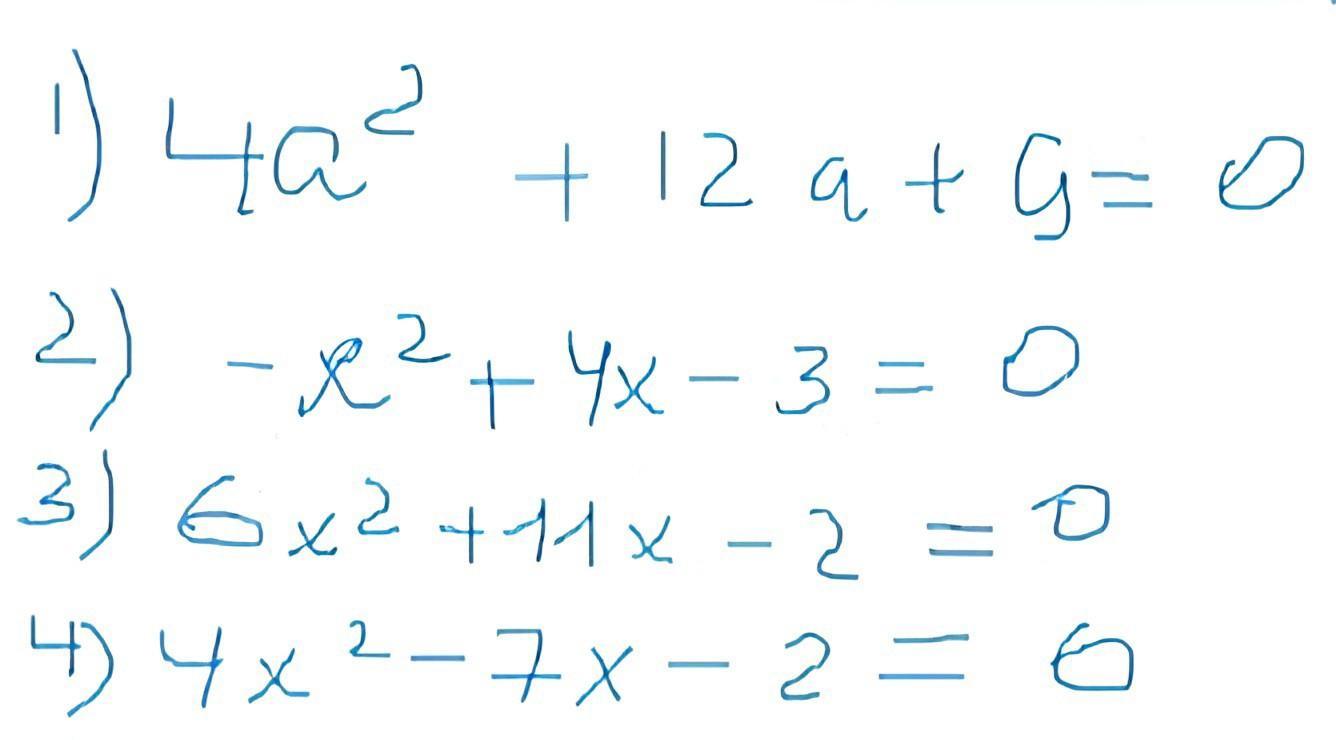Срочно пожалуйста! Плачу 25 баллов!​

У тебя есть многочлен второй степени вида [tex]ax^2 + bx + c = 0[/tex]. Дискриминант D = [tex]b^2 - 4ac[/tex].
Корни уравнения (два, когда D > 0, один, когда D = 0, действительные корни отсутствуют при D < 0) ищутся как

[tex]x_1 = (-b + \sqrt{D}) / (2a)[/tex],

[tex]x_2 = (-b - \sqrt{D}) / (2a)[/tex], тогда

1) D = [tex]12^2 - 4*4*9 = 144 - 144 = 0[/tex],
a = -12 / (2*4) = -12/8 = -3/2 = -1.5

2) D = [tex]4^2 - 4*(-1)*(-3) = 4[/tex].

[tex]x_1 = (-4 + \sqrt{4}) / (2*(-1)) = 1[/tex],

[tex]x_2 = (-4 - \sqrt{4}) / (2*(-1)) = 3.[/tex]

3) D = [tex]11^2 - 4*6*(-2) = 121 + 48 = 169[/tex].

[tex]x_1 = (-11 + \sqrt{169}) / (2*6) = 2/12[/tex] = [tex]1/6[/tex],

[tex]x_2 = (-11 - \sqrt{169}) / (2*6) = -2[/tex].

4) D = [tex](-7)^{2} - 4*4*(-2) = 49 + 32 = 81[/tex].

[tex]x_1 = (7 + \sqrt{81}) / (2*4) = 16 / 8 = 2[/tex],

[tex]x_2 = (7 - \sqrt{81}) / (2*4) = -2 / 8 = -1/4 = -0.25[/tex].