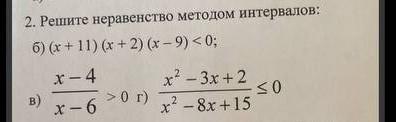2. Решите неравенство методом интервалов 6) (x + 11) (x + 2) (x-9) < 0; в) x-4 x-6 30 г) x² -3x+2 x² -8x+15 ≤0
​

б)

[tex](x + 11)(x + 2)(x - 9) < 0 \\ - - - ( - 11) + + + ( - 2) - - - (9) + + + \\ x \:\epsilon \: ( - \propto; \: - 11)U( - 2; \: 9)[/tex]

в)

[tex] \frac{x - 4}{x - 6} > 0 \\ (x - 4)(x - 6) > 0 \\ + + + (4) - - - (6) + + + \\ x \: \epsilon \: ( - \propto; \: 4)U(6; \: + \propto)[/tex]

г)

[tex]po \: \: \: teoreme \: \: \: vieta \\ {x}^{2} + bx + c = 0\\ x_{1} + x_{2} = - b\\ x_{1} x_{2} = c \\ \\ {x {}^{2} - 3x + 2}^{} = 0 \\ x_{1} + x_{2} =3 \\ x_{1} x_{2} =2 \\ x_{1} = 1\\ x_{2} = 2 \\ x {}^{2} - 3x + 2 = (x - 1)(x - 2) \\ \\ {x}^{2} - 8x + 15 \\ x_{1} + x_{2} =8 \\ x_{1} x_{2} = 15 \\ x_{1} = 3 \\ x_{2} = 5 \\ {x}^{2} - 8x + 15 = (x - 3)(x - 5) \\ \\ \frac{ {x}^{2} - 3x + 2 }{ {x}^{2} - 8x + 15 } \leqslant 0 \\ \frac{(x - 1)(x - 2)}{(x - 3)(x - 5)} \leqslant 0 \\ \\ \left \{ {{(x - 1)(x - 2)(x - 3)(x - 5) \leqslant 0} \atop {x \neq3 \: \: \: \: and \: \: \: \: x\neq5}} \right. \\ \\ + + + [1] - - - [2] + + + (3) - - - (5) + + + \\ x \:\epsilon \: [1; \: 2]U(3; \: 5)[/tex]