СРОЧНО ДАЮ 30 БАЛОВ Периметр трикутника ABC дорівнює 48. Знайти сторону ВС, якщо якщо NC- BN=2, AM=8. A M R 0 0 K N C​

Ответ:

Сторона ВС дорівнює 16 ед

Объяснение:

Периметр трикутника ABC дорівнює 48. Знайти сторону ВС, якщо якщо NC- BN=2, AM=8.

• Відрізки дотичних, проведених з однієї точки до кола, рівні.

Розв'язання

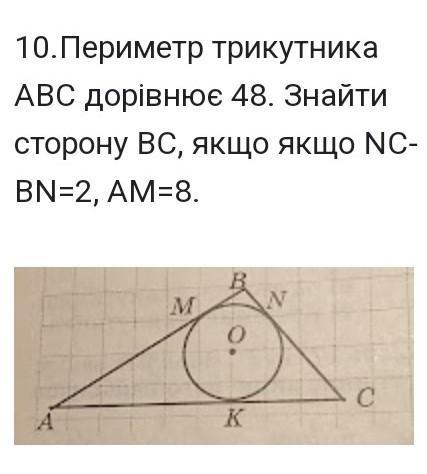
Нехай АВС - даний трикутник, M, N, K - точки дотику вписаного кола до сторін AB, BC і AC відповідно.

АМ = 8, NC-BN=2.

Нехай BN=x, тоді NC=BN+2= x+2.

За властивістю дотичних, проведених до кола з однієї точки, маємо:

MB=BN=x

KC=NC=x+2

AK=AM=8

За аксиомою вимірювання відрізків отримаємо:

AB = AM+MB = 8+х

BC = BN+NC = х+х+2 = 2х+2

АС = АК+КС = 8+х+2 = х+10

Периметр трикутника ABC:

P = AB+BC+AC = 8+x+2x+2+x+10 = 4x+20

За умовою периметр дорівнює 48, складаємо рівняння:

4х+20=48

4х=28

х=7

Отже, ВС = 2 • 7 + 2 = 16 (ед)

Відповідь: 16 ед.

#SPJ1