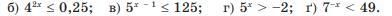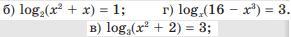Ответы 2
Ответ:
[tex] {4}^{2x} \leqslant 0.25 \\ {2}^{4x} \leqslant {2}^{ - 2} \\ 4x \leqslant - 2 \\ x \leqslant - 0.5[/tex]
[tex] {5}^{x - 1} \leqslant 125 \\ {5}^{ x - 1} \leqslant {5}^{3} \\ x - 1 \leqslant 3 \\ x \leqslant 4[/tex]
[tex] {5}^{x} > - 2[/tex]
x - любое
[tex] {7}^{ - x} < 49 \\ {7}^{ - x} < {7}^{2} \\ - x < 2 \\ x > 2[/tex]
Ответ:
ответ смотри на фотографии
Премиум статус
Получайте самые быстрые
ответы на свои вопросы
ответы на свои вопросы
У вас остались
вопросы?
вопросы?
