В прямоугольнике ABCD окружность с центром т.О. АТ;ВН;СК;DM - касательные. АТ=34см; ВН=31см; СК=46см. Найдите касательную DM.​

Ответ:

(см. объяснение)

Объяснение:

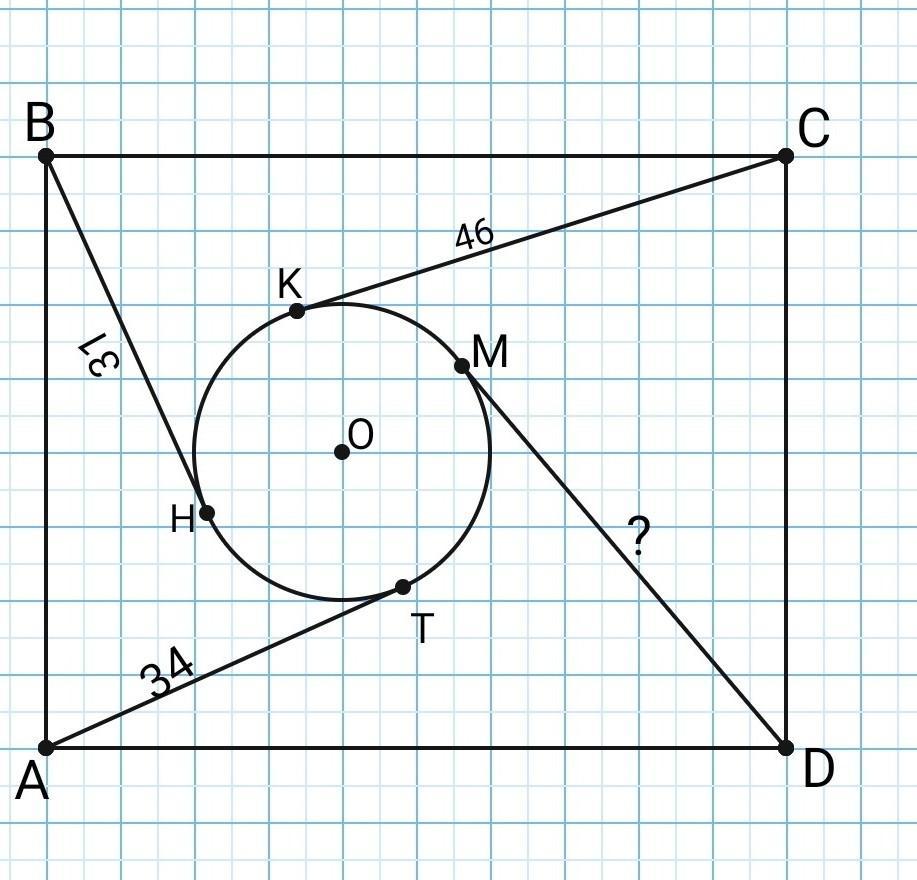
Соединим BO и OH. Получим треугольник BOH:

Он прямоугольный, так как [tex]\angle BHO=90^\circ[/tex], а его сторона [tex]OH[/tex] равна [tex]r[/tex] - радиусу окружности.

Тогда по теореме Пифагора для этого треугольника найдем [tex]BO^2:[/tex]

[tex]BO^2=31^2+r^2[/tex]

Аналогично из треугольников [tex]AOT[/tex], [tex]COK[/tex] и [tex]DOM[/tex] имеем:

[tex]AO^2=34^2+r^2,\;CO^2=46^2+r^2,\;DO^2=x^2+r^2[/tex] (здесь [tex]x=DM[/tex])

Теперь проведем через центр окружности O прямые, параллельные сторонам прямоугольника BC и AB. Пусть они пересекают прямоугольник в точках [tex]J,\;E,\;G,\;I[/tex] (см. рисунок).

Введем обозначения:

[tex]BE=AI=w,\;BJ=CG=q,\;JA=GD=z,\;EC=ID=p[/tex]

Понятно, что треугольники [tex]BOE,\;OEC,\;JOA,\;ODI[/tex] прямоугольные.

Запишем для каждого из них теорему Пифагора и получим систему:

[tex]\left\{\begin{array}{c}\left(31^2+r^2\right)-q^2=w^2\\\left(46^2+r^2\right)-q^2=p^2\\\left(34^2+r^2\right)-w^2=z^2\\\left(x^2+r^2\right)-z^2=p^2\end{array}\right;[/tex]

Выразим из последней строки системы [tex]x^2:[/tex]

[tex]x^2=p^2+z^2-r^2[/tex]

Подставляем [tex]p^2[/tex] из второй строки системы:

[tex]x^2=46^2+r^2-q^2+z^2-r^2=46^2-q^2+z^2[/tex]

Подставляем [tex]z^2[/tex] из третьей строки системы:

[tex]x^2=46^2-q^2+34^2+r^2-w^2[/tex]

Подставляем [tex]w^2[/tex] из первой строки системы:

[tex]x^2=46^2-q^2+34^2+r^2-31^2-r^2+q^2=46^2+34^2-31^2=2311[/tex]

Получили, что [tex]DM=\sqrt{2311}[/tex].

Задание выполнено!