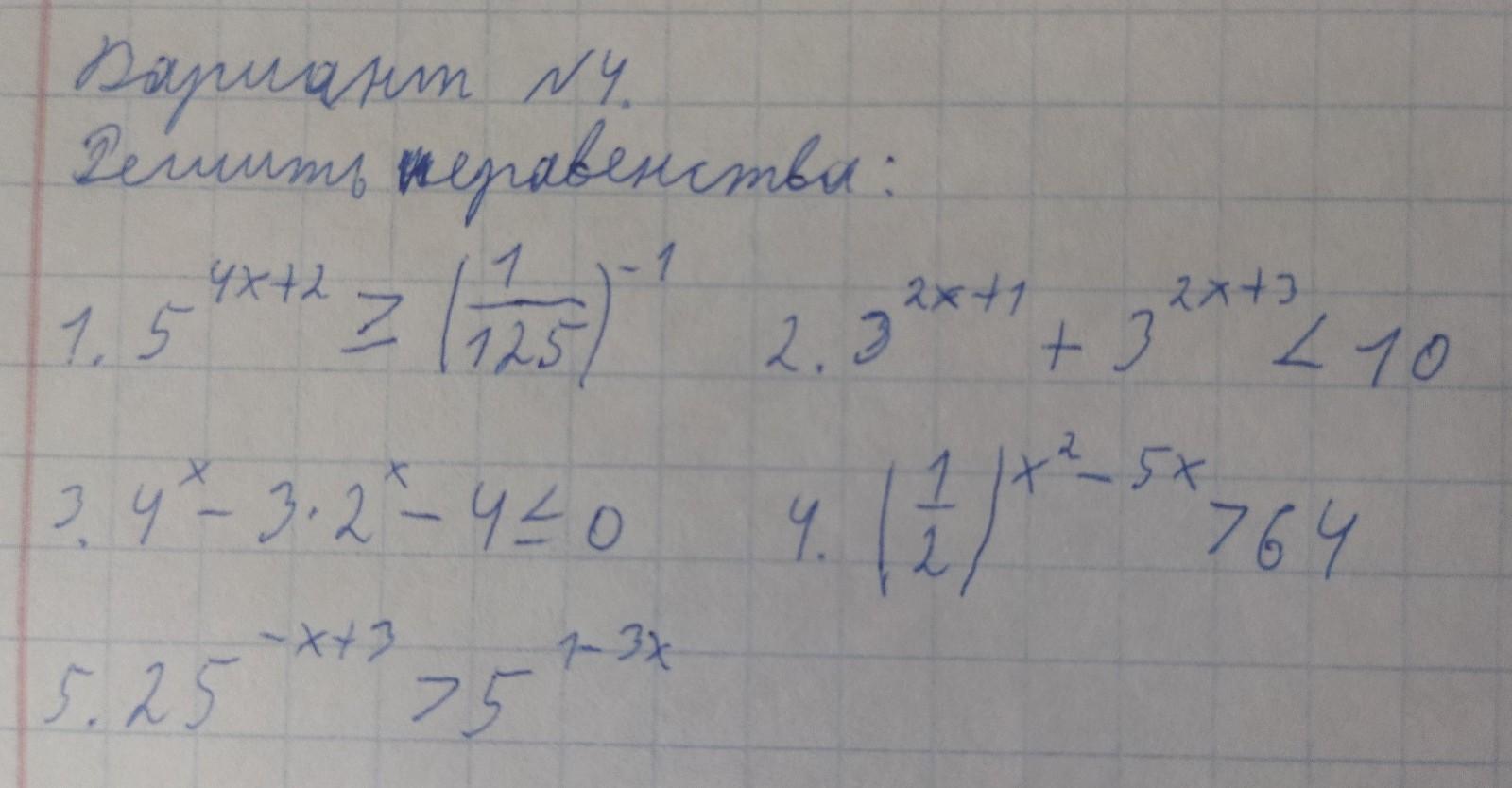Ответы 1
Ответ:
1. x ∈ [1/4; +∞)
2. x ∈ (-∞; -1/2)
3. x ∈ (-∞; 2]
4. х ∈ (2; 3)
5. x ∈ (-5; +∞)
Объяснение:
Решить неравенства:
[tex]\displaystyle \bf 1.\;5^{4x+2}\geq \left(\frac{1}{125}\right)^{-1}[/tex]
[tex]\displaystyle \bf \boxed { a^{-n}=\frac{1}{a^n} }[/tex]
[tex]\displaystyle 5^{4x+2}\geq 125\\\\5^{4x+2}\geq 5^3[/tex]
Основание степени 5 > 1 ⇒ функция возрастает.
⇒ 4x + 2 ≥ 3
4x ≥ 1 |:4
x ≥ 1/4
x ∈ [1/4; +∞)
[tex]\displaystyle \bf 2.\;3^{2x+1}+3^{2x+3} < 10[/tex]
[tex]\displaystyle \bf \boxed { a^{m}\cdot a^n=a^{m+n}}[/tex]
[tex]\displaystyle 3^{2x+1}+3^{2x+1+2} < 10\\\\3^{2x+1}+3^{2x+1}\cdot 3^2 < 10\\\\3^{2x+1}+9\cdot3^{2x+1} < 10\\\\10\cdot3^{2x+1} < 10\;\;\;\;\;|:10\\\\3^{2x+1} < 1\\\\3^{2x+1} < 3^0[/tex]
Основание степени 3 > 1 ⇒ функция возрастает.
⇒ 2x + 1 < 0
2x < -1 |:2
x< -1/2
x ∈ (-∞; -1/2)
[tex]\displaystyle \bf 3.\; 4^x-3\cdot2^x-4\leq 0[/tex]
[tex]\displaystyle \bf \boxed { (a^{m})^n=a^{mn}}[/tex]
[tex]\displaystyle (2^2)^x-3\cdot2^x-4\leq 0\\\\2^ {2x} -3\cdot2^x-4\leq 0[/tex]
Замена переменной:
2ˣ = t, t > 0
t² - 3t - 4 ≤ 0
Решим методом интервалов. Найдем корни уравнения
t² - 3t - 4 = 0
По теореме Виета:
х₁ = 4; х₂ = -1
Отметим их на числовой оси и определим знаки на промежутках:
[tex]+++[-1]---[4]+++[/tex]
t > 0 ⇒ 0 < t ≤ 4
Обратная замена:
0 < 2ˣ ≤ 2²
Основание степени 2 > 1 ⇒ функция возрастает.
⇒ x ≤ 2
x ∈ (-∞; 2]
[tex]\displaystyle \bf 4.\;\left(\frac{1}{2}\right)^{x^2-5x} > 64[/tex]
[tex]\displaystyle \left(\frac{1}{2}\right)^{x^2-5x} > 2^6\\\\\left(\frac{1}{2}\right)^{x^2-5x} > \left(\frac{1}{2}\right)^{-6}[/tex]
Основание степени 0 < 1/2 < 1 ⇒ функция убывает. Знак неравенства перевернется.
х² - 5х < -6
x² - 5x + 6 < 0
Корни по теореме Виета:
х₁ = 2; х₂ = 3
[tex]+++(2)---(3)+++[/tex]
х ∈ (2; 3)
[tex]\displaystyle \bf 5.\;25^{-x+3} > 5^{1-3x}\\\\[/tex]
[tex](5^2)^{-x+3} > 5^{1-3x}\\\\5^{-2x+6} > 5^{1-3x}[/tex]
Основание степени 5 > 1 ⇒ функция возрастает.
⇒ -2x + 6 > 1 - 3x
x > -5
x ∈ (-5; +∞)
#SPJ1
ответы на свои вопросы

вопросы?
по алгебре