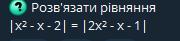Алгебра. Даю 42 бали.

Вирішити 3 завдання.

Объяснение:

1.

|х²-х-2|=|2х²-х-1|

х²-х-2=2х²-х-1

х²-х-2= -(2х²-х-1)

х²= -1

3х²-2х-3=0

х∉R

x=(1+√10)/3

x=(1-√3)/3

объединение:

х=(1+√10)/3

х=(1-√10)/3

ответ: х1=(1-√10)/3; х2=(1+√10)/3

2.

|х³+х+1|=1

х³+х+1=1

х³+х+1= -1

х³+х=0

х³+х+1+1=0

х(х²+1)=0

х³+х+2+х²-х²=0

х=0 ; х²= -1

х³-х+2х+2+х²-х²=0

х=0; х∉R

x²(x+1)-x(x+1)+2(x-1)=0

x=0 ; x∉R

(x+1)(x²-x+2)=0

x=0;x∉R

x= -1 ; x∉R

0бьединие:

х=0

х= -1

ответ: х1= -1 ; х2=0

3.

|х-2|=|2х-1|

х-2=2х-1

х-2= -(2х-1)

х-2-2х= -1

х-2+2х=1

-х=1

3х=3

х= -1

х=1

ответ: х1= -1; х2= 1

Ответ:

Решить уравнения с модулями .

Под знаком модуля может стоять как положительное выражение, так и отрицательное , или 0 . А сам модуль принимает только неотрицательные значения .

[tex]\bf 1)\ \ |x^2-x-2|=|2x^2-x-1|\ \ \ \Rightarrow \ \ \ x^2-x-2=\pm (2x^2-x-1)\\\\a)\ \ x^2-x-2=2x^2-x-1\ \ \ ,\ \ \ x^2+1=0\ \ ,\ \ x^2=-1\ \ \Rightarrow \ \ x\in \varnothing \\\\b)\ \ x^2-x-2=-2x^2+x+1\ \ ,\ \ \ 3x^2-2x-3=0\ \ ,\\\\D/4=(b/2)^2-ac=1+9=10\ \ ,\ \ x_{1,2}=\dfrac{1\pm \sqrt{10}}{3}\\\\Otvet:\ x_1=\dfrac{1-\sqrt{10}}{3}\ ,\ \ x_2=\dfrac{1+\sqrt{10}}{3}\ .[/tex]  

[tex]\bf 2)\ \ |x^3+x+1|=1\ \ \ \Rightarrow \ \ \ x^3+x+1=\pm 1\\\\a)\ \ x^3+x+1=1\ \ ,\ \ x^3+x=0\ \ ,\ \ x\, (\underbrace{\bf x^2+1}_{\geq 1})=0\ \ \to \ \ x_1=0\\\\b)\ \ x^3+x+1=-1\ \ ,\ \ x^3+x+2=0\ \ ,\\\\x^2(x+1)-x^2+(x+1)+1=0\ \ ,\ \ x^2(x+1)+(x+1)-(x^2-1)=0\ ,\\\\x^2(x+1)+(x+1)-(x-1)(x+1)=0\\\\(x+1)(x^2+1-(x-1))=0\ \ ,\ \ (x+1)(x^2-x+2)=0\ \ ,\\\\x+1=0\ \ \to \ \ x_2=-1\\\\x^2-x+2=0\ \ ,\ \ D=1-4\cdot 2=-7 < 0\ \ \Rightarrow \ \ x\in \varnothing[/tex]  

нет действительных корней .  

[tex]\bf Otvet:\ x_1=0\ ,\ x_2=-1\ .[/tex]    

[tex]\bf 3)\ \ |x-2|=|2x-1|\ \ \ \Rightarrow \ \ \ |x-2|^2=|2x-1|^2\ \ ,\\\\\star \ \ |a|^2=a^2\ \ \star \\\\(x-2)^2=(2x-1)^2\ \ ,\ \ \ (x-2)^2-(2x-1)^2=0[/tex]  

Применяем формулу разности квадратов .

[tex]\bf (x-2-2x+1)(x-2+2x-1)=0\ \ ,\\\\(-x-1)(3x-3)=0\ \ ,\\\\-x-1=0\ \ \to \ \ x=-1\\\\3x-3=0\ \ \ \to \ \ \ x=1\\\\Otvet:\ x_1=-1\ ,\ x_2=1\ .[/tex]