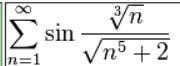Дослідити ряд на збіжність

Ответ:

• ряд [tex]\displaystyle \sum\limits_{n=1}^\infty \sin\frac{\sqrt[3]{n} }{\sqrt{n^5+2} }[/tex] сходится

Пошаговое объяснение:

Дан ряд:

[tex]\displaystyle \sum\limits_{n=1}^\infty \sin\frac{\sqrt[3]{n} }{\sqrt{n^5+2} }[/tex]

Сравним данный ряд с рядом [tex]\displaystyle \sum\limits_{n=1}^\infty \frac{1}{\sqrt[6]{n^{13}} }[/tex] - это гармонический сходящийся ряд, так как [tex]\displaystyle \alpha =\frac{13}{6} > 1[/tex].

Используем предельный признак сравнения:

[tex]\large \boldsymbol{} \displaystyle \lim_{n \to \infty} \frac{\sin\frac{\sqrt[3]{n} }{\sqrt{n^5+2} }}{\frac{1}{\sqrt[6]{n^{13}} } } =\lim_{n \to \infty}\bigg(\sqrt[6]{n^{13}}\cdot \sin\frac{\sqrt[3]{n} }{\sqrt{n^5+2} }\bigg)=\\=\bigg[\sin\frac{\sqrt[3]{n} }{\sqrt{n^5+2} }\sim \frac{\sqrt[3]{n} }{\sqrt{n^5+2} } \bigg]=\lim_{n \to \infty}\bigg(\sqrt[6]{n^{13}}\cdot\frac{\sqrt[3]{n} }{\sqrt{n^5+2} }\bigg)=\\[/tex]

[tex]\large \boldsymbol{} \displaystyle =\lim_{n \to \infty} \bigg( \frac{n^{\frac{13}{6}+\frac{1}{3} }} {\sqrt{n^5+2} }\bigg)=\lim_{n \to \infty} \bigg( \frac{n^{\frac{5}{2} }} {\sqrt{n^5+2} }\bigg)=\\=\bigg[\sqrt{n^5+2}\sim \sqrt{n^5} \bigg]=\lim_{n \to \infty} \bigg( \frac{ \sqrt{n^5} } {\sqrt{n^5} }\bigg)=1[/tex]

Поскольку предел оказался равным конечному числу и поскольку сравнимый ряд [tex]\displaystyle \sum\limits_{n=1}^\infty \frac{1}{\sqrt[6]{n^{13}} }[/tex] сходится, то и исходный ряд [tex]\displaystyle \sum\limits_{n=1}^\infty \sin\frac{\sqrt[3]{n} }{\sqrt{n^5+2} }[/tex] тоже сходится.

Проясним некоторые моменты:

1) Почему выбрали именно такой [tex]\displaystyle \sum\limits_{n=1}^\infty \frac{1}{\sqrt[6]{n^{13}} }[/tex] сравнимый ряд?

Способ нахождения сравнимого ряда достаточно стандартен: надо из наибольшего показателя степени знаменателя вычесть наибольший показатель степени числителя.

В знаменателе под корнем стоит выражение [tex]n^5+2[/tex], большая степень - 5. Мы мысленно отбрасываем 2, и тогда наибольший показатель степени знаменателя получится [tex]\displaystyle \frac{5}{2}[/tex] ([tex]\displaystyle \sqrt{n^5}= n^{\frac{5}{2} }[/tex]). (Если бы было, к примеру, подкоренное выражение [tex]n^5+n^3+2[/tex], мы бы отбросили [tex]n^3+2[/tex], так как 5 - по-прежнему наибольшая степень).

В числителе попроще: сразу видно, что наибольший показатель степени - [tex]\displaystyle \frac{1}{3}[/tex] ([tex]\displaystyle \sqrt[3]{n} =n^\frac{1}{3}[/tex]).

В качестве сравнимого ряда обычно выбирают гармонический ряд [tex]\displaystyle \sum\limits_{n=1}^\infty \frac{1}{n^\alpha }[/tex], тогда по приведенному способу вначале этого пункта найдем [tex]\alpha[/tex]: [tex]\displaystyle \alpha =\frac{5}{2} -\frac{1}{3} =\frac{13}{6}[/tex]. Таким образом, сравнимый ряд: [tex]\displaystyle \sum\limits_{n=1}^\infty \frac{1}{n^{\frac{13}{6} } }=\displaystyle \sum\limits_{n=1}^\infty \frac{1}{\sqrt[6]{n^{13}} }[/tex].

2) Каким образом заменили [tex]\displaystyle \sin\frac{\sqrt[3]{n} }{\sqrt{n^5+2} }[/tex] на [tex]\displaystyle\frac{\sqrt[3]{n} }{\sqrt{n^5+2} }[/tex]?

Заметим, что [tex]\sqrt{n^5+2}[/tex] более высокого порядка роста, чем [tex]\sqrt[3]{n}[/tex], проще говоря, знаменатель дроби растет быстрее (причем во много раз), чем числитель, поэтому дробь (аргумент синуса) можно считать бесконечно малой. Но из курса математического анализа известно, что для [tex]\alpha \rightarrow 0[/tex] справедлива следующая эквивалентность: [tex]\sin\alpha \sim \alpha[/tex].

3) Каким образом заменили [tex]\sqrt{n^5+2}[/tex] на [tex]\sqrt{n^5}[/tex]?

Посмотрим на предел, который идет до замены: [tex]\large \boldsymbol{} \displaystyle \lim_{n \to \infty} \bigg( \frac{n^{\frac{5}{2} }} {\sqrt{n^5+2} }\bigg)[/tex].

Можно заметить, что так как и в числителе, и в знаменателе основание с наибольшим показателем степени - [tex]\displaystyle n^{\frac{5}{2} }[/tex], то [tex]\sqrt{n^5}[/tex] и [tex]\sqrt{n^5+2}[/tex] называются функциями одного порядка роста. А для таких функций при [tex]n\rightarrow \infty[/tex] справедливо следующее: [tex]an+b\sim an[/tex], [tex]an^2+bn+c\sim an^2[/tex] и т.д.

Данный способ крайне удобен для вычисления подобных пределов, так как мы практически сразу получаем ответ.

Как бы выглядело полное решение данного предела?

[tex]\large \boldsymbol{} \displaystyle \lim_{n \to \infty} \bigg( \frac{n^{\frac{5}{2} }} {\sqrt{n^5+2} }\bigg)=\lim_{n \to \infty} \bigg( \frac{\sqrt{n^5} } {\sqrt{n^5(1+\frac{2}{n^5} )} }\bigg)=\\=\lim_{n \to \infty} \bigg( \frac{\sqrt{n^5} } {\sqrt{n^5} \sqrt{1+\frac{2}{n^5} } }\bigg)=\lim_{n \to \infty} \bigg( \frac{1} {\sqrt{1+\frac{2}{n^5}}\rightarrow 0 }\bigg)=\frac{1}{\sqrt{1+0} } =1[/tex]

#SPJ1