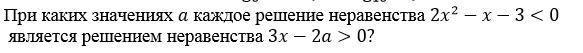При каких значениях a каждое решение неравенства 2x^2-x-3<0
является решением неравенства 3x-2a>0?

Ответ:

а ∈ (-∞; -1,5]

Объяснение:

Разложим левую часть квадратного неравенства на множители:

2·x²-x-3 < 0 ⇔ 2·x²-2-x-1 < 0 ⇔ 2·(x²-1)-(x+1) < 0 ⇔

⇔ 2·(x-1)·(x+1)-(x+1) < 0 ⇔  (2·x-2-1)·(x+1) < 0 ⇔  (2·x-3)·(x+1) < 0 ⇔

⇔  2·(x-1,5)·(x+1) < 0.

Применим метод интервалов: точки x = -1 и x = 1,5 делят числовую ось на интервалы (-∞; -1), (-1; 1,5), (1,5; +∞),  внутри которых квадратный трёхчлен не меняет знак.

Проверим знаки квадратного трёхчлена на каждом интервале:

1) пусть x = -2 ∈ (-∞; -1), то 2·(-2)² - (-2) - 3 = 7 > 0 - положительно, не подходит;

2) пусть x = 0 ∈ (-1; 1,5), то 2·0² - 0 - 3 = -3 < 0 - отрицательно, подходит;

3) пусть x = 2 ∈ (1,5; +∞), то 2·2² - 2 - 3 = 3 > 0 - положительно, не подходит.

Отсюда, числа из интервала (-1; 1,5) являются решением неравенства 2·x²-x-3 < 0.

По условию каждое решение неравенства 2·x²-x-3 < 0 должен быть решением 3·x-2·a > 0, то есть множество (-1; 1,5) должен быть подмножеством решений неравенства 3·x-2·a > 0.

Решаем линейное неравенство

3·x-2·a > 0 ⇔ 3·x > 2·a ⇔ [tex]\tt x > \dfrac{2 \cdot a}{3} \Leftrightarrow x \in ( \dfrac{2 \cdot a}{3}; +\infty).[/tex]

Значит, нужно найти такие значения a, при которых

[tex]\tt (-1; 1,5) \subset ( \dfrac{2 \cdot a}{3}; +\infty).[/tex]

Это может быть, когда

[tex]\tt \dfrac{2 \cdot a}{3} \leq -1.[/tex]

Из последнего неравенства получим:

2·а ≤ -3 ⇔ а ≤ -1,5 ⇔ а ∈ (-∞; -1,5].

#SPJ1