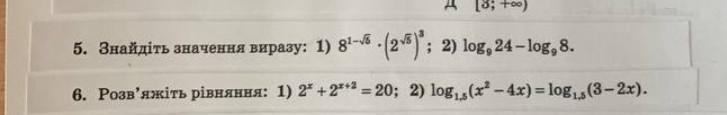Помогите пожалуйста Задание 6 на фото​

[tex]\displaystyle\bf\\1)\\\\2^{x} +2^{x+2}=20\\\\2^{x} \cdot(1+2^{2} )=20\\\\2^{x} \cdot 5=20\\\\2^{x} =4\\\\2^{x} =2^{2} \\\\\boxed{x=2}\\\\2)\\\\\log_{1,5} (x^{2} -4x)=\log_{1,5} (3-2x)\\\\ODZ:\\\\\left \{ {{x^{2} -4x > 0} \atop {3-2x > 0}} \right. \\\\\\\left \{ {{x(x-4) > 0} \atop {2x < 3}} \right.\\\\\\\left \{ {{x\in(-\infty ; \ 0)\cup(4 \ ; \ +\infty)} \atop {x < 1,5}} \right. \ \ \Rightarrow \ \ x\in(-\infty \ ; \ 0)\\\\\\x^{2} -4x=3-2x\\\\x^{2}-2x-3=0[/tex]

[tex]\displaystyle\bf\\Teorema \ Vieta \ :\\\\x_{1}+ x_{2} =2\\\\x_{1} \cdot x_{2} =-3\\\\x_{1} =-1\\\\x_{2} =3 \ - \ ne \ podxodit\\\\Otvet \ : \ -1[/tex]