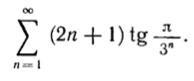Срочно!!!Допоможіть будь ласка

Ответ:

Для определения сходимости ряда   применим достаточный признак Даламбера .

[tex]\bf \displaystyle \sum \limits _{n-1}^{\infty }\, (2n+1)\cdot tg\frac{\pi }{3^{n}}\\\\\\\lim_{n \to \infty}\, \frac{a_{n+1}}{a_{n}}=\lim\limits_{n \to \infty}\frac{ (2n+3)\cdot tg\dfrac{\pi }{3^{n+1}}}{ (2n+1)\cdot tg\dfrac{\pi }{3^{n}}}=\Big[\ tg\, \alpha (x)\sim \alpha (x)\ ,\ \ \alpha (x)\to 0\ \Big]=[/tex]  

[tex]\bf \displaystyle =\lim\limits_{n \to \infty}\frac{(2n+3)\cdot \dfrac{\pi }{3^{n+1}}}{(2n+1)\cdot \dfrac{\pi }{3^{n}}}=\lim\limits_{n \to \infty}\Big(\, \frac{2n+3}{2n+1}\cdot \frac{3^{n}}{3^{n}\cdot 3}\left)=\lim\limits_{n \to \infty}\Big(1\cdot \frac{1}{3}\Big)=\frac{1}{3} < 1[/tex]  

Получили предел, меньший 1 , значит ряд сходится .