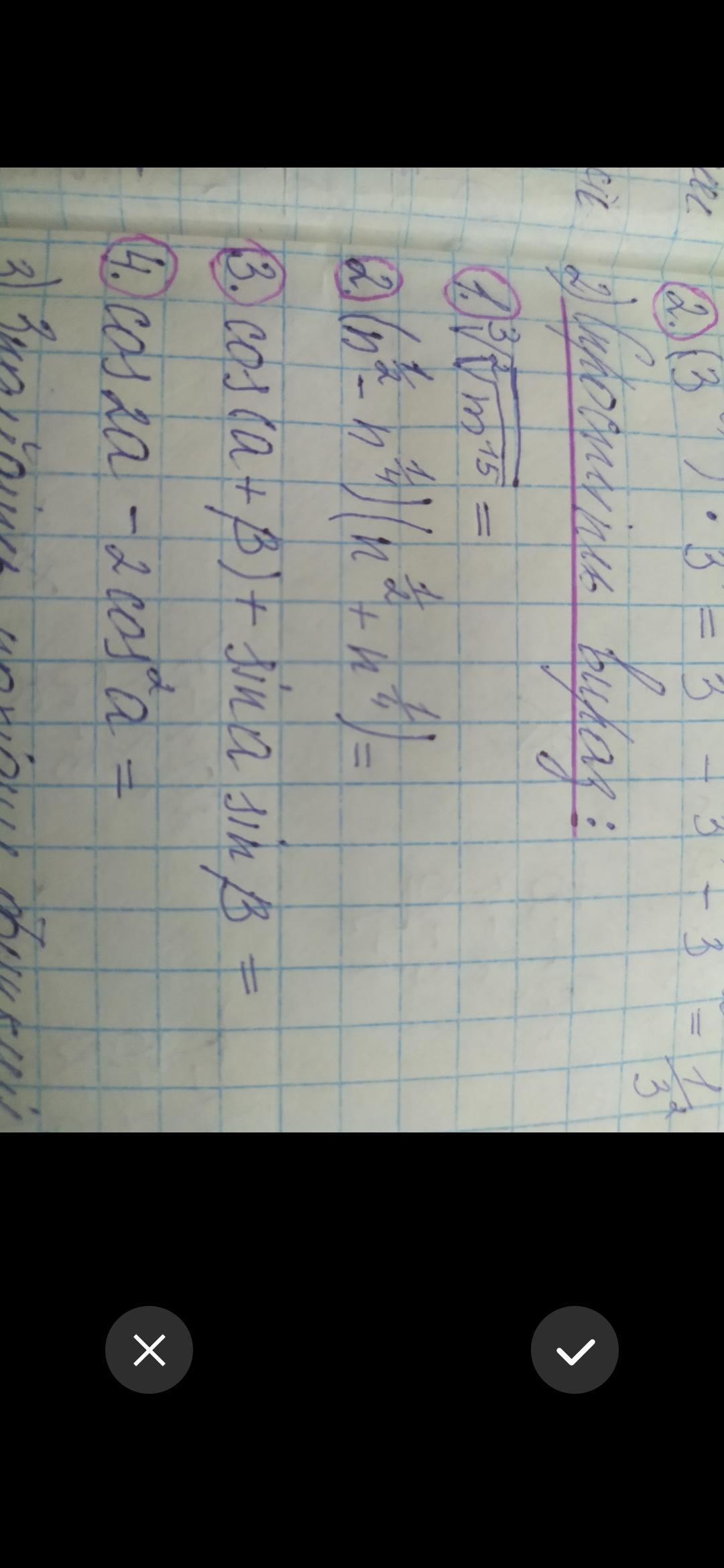Помогите пожалуйста разобраться срочно очень!!!

Ответ:

Упростить выражения .  Применяем свойства степеней и корней , а также тригонометрические формулы косинуса суммы , косинуса двойного угла .

[tex]\bf 1)\ \ \sqrt[3]{\sqrt[2]{m^{15}}}=\sqrt[3]{\sqrt{m^{15}}}=\sqrt[6]{m^{15}}=\sqrt{m^{5}}\\\\2)\ \ \Big(n^{\frac{1}{2}}-n^{\frac{1}{4}}\Big)\Big(n^{\frac{1}{2}}+n^{\frac{1}{4}}\Big)=\Big(n^{\frac{1}{2}}\Big)^2-\Big(n^{\frac{1}{4}}\Big)^2=n-n^{\frac{1}{2}}\\\\3)\ \ cos(\alpha +\beta )+sin\alpha \cdot sin\beta =cos\alpha \cdot cos\beta -sin\alpha \cdot sin\beta +sin\alpha \cdot sin\beta =\\\\=cos\alpha \cdot cos\beta \\\\4)\ \ cos2\alpha -2\, cos^2\alpha =(cos^2\alpha -sin^2\alpha )-2cos^2\alpha =[/tex]  

[tex]\bf =cos^2\alpha -(1-cos^2\alpha )-2cos^2\alpha =cos^2\alpha -1+cos^2\alpha -2cos^2\alpha =-1[/tex]