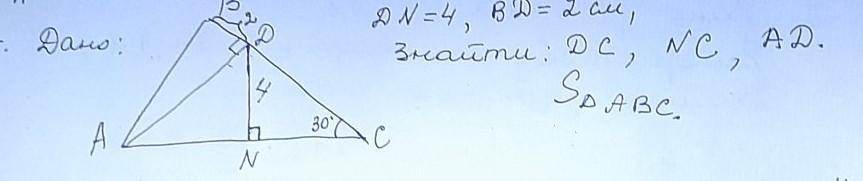Дано: ДN=4, BD=2см, Знайти: DC,NC,AD. Sadc.​

Ответ:

За теоремою Піфагора в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Так як маємо трикутник з прямим кутом D, то можемо скористатись цією теоремою:

AD² = BD² + AB²

Але нам потрібно знайти AD, а не AD². Тож використовуючи операцію взяття квадратного кореня, отримаємо:

AD = √(BD² + AB²)

Тепер застосуємо формули для знаходження значень сторін трикутника SADC (SADC - прямокутний трикутник, бо кут A - прямий):

DC = AB = DN - NC = 4 - 2 = 2 см

NC = BD = 2 см

AD = √(BD² + AB²) = √(2² + 4²) = √20 см

Отже,

DC = 2 см,

NC = 2 см,

AD = √20 см.

Також нам потрібно знайти площу трикутника SADC. Вона розраховується за формулою:

SADC = (AD * DC) / 2

Підставляючи в цю формулу відповідні значення, отримаємо:

SADC = (√20 см * 2 см) / 2 = √20 см² ≈ 4,47 см².

Объяснение: