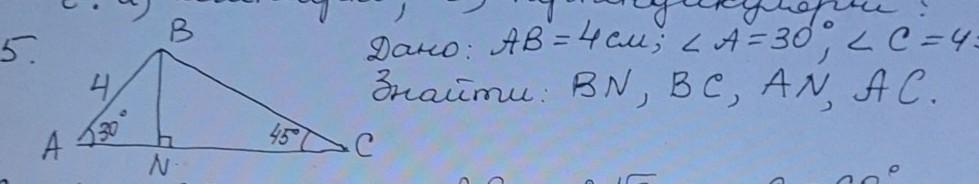дано: AB=4см; A=30, LC=45 Знайти: BN,BC,AN,AC. ​

Объяснение:

Розглянемо трикутник АВN, катет BN лежить навпроти кута рівного 30⁰, значить він дорівнює половині гіпотенузи, тобто BN=4:2=2см.

за теоремою Піфагора знайдемо АN=

[tex] \sqrt{ {4}^{2} - {2}^{2} } = \sqrt{12} = 2 \sqrt{3} cm[/tex]

Розглянемо ∆ВNC, кут С=45⁰, значить кутВ=90-45=45⁰. значить що цей трикутник рівнобічний. BN=NC=2см.

за теоремою Піфагора знайдемо ВС=

[tex] \sqrt{ {2}^{2} + {2}^{2} } = \sqrt{8 } = 2 \sqrt{2} cm[/tex]

AC=AN+NC= 2√3+2 см=2(1+√3)см

відповідь: BN=2см, ВС=2√2см, АN=2√3см, АС=2(1+√3)см