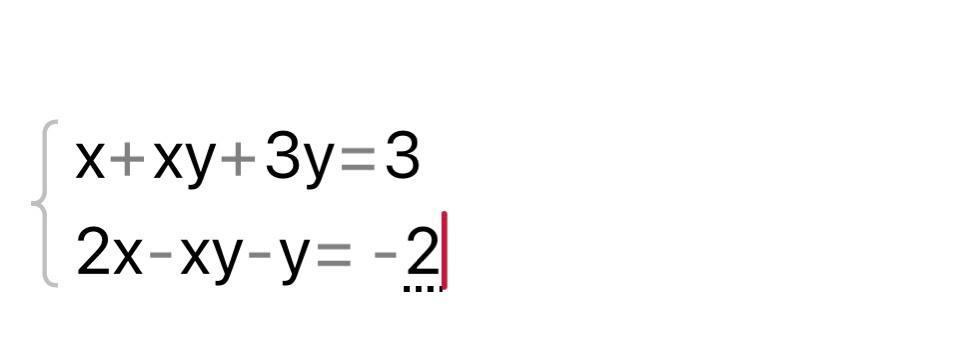допоможіть будь ласка терміново треба вирішити це рівняння

Ответ:

Решить систему уравнений .

[tex]\left\{\begin{array}{l}\bf x+xy+3y=3\\\bf 2x-xy-y=-2\end{array}\right\ \ \left\{\begin{array}{l}\bf xy=3-x-3y\\\bf xy=2x-y+2\end{array}\right\ \ \left\{\begin{array}{l}\bf 3-x-3y=2x-y+2\\\bf xy=2x-y+2\end{array}\right\\\\\\\left\{\begin{array}{l}\bf 3x+2y=1\\\bf xy=2x-y+2\end{array}\right\ \ \left\{\begin{array}{l}\bf y=\dfrac{1}{2}-\dfrac{3}{2}\, x\\\bf xy=2x-y+2\end{array}\right[/tex]  

[tex]\bf xy=2x-y+2\ \ \Rightarrow \ \ \ x\cdot \Big(\dfrac{1}{2}-\dfrac{3}{2}\, x\Big)=2x-\dfrac{1}{2}+\dfrac{3}{2}\, x+2\ \ ,\\\\\\0,5x-1,5x^2=2x-0,5+1,5x+2\\\\1,5x^2+3x+2=0\ \ \Big|\cdot 2\\\\3x^2+6x+4=0\\\\D/4=(b/2)^2-ac=3^2-3\cdot 4=-3 < 0[/tex]  

Так как  D<0 , то нет действительный корней .

Ответ: система не имеет действительных решений .