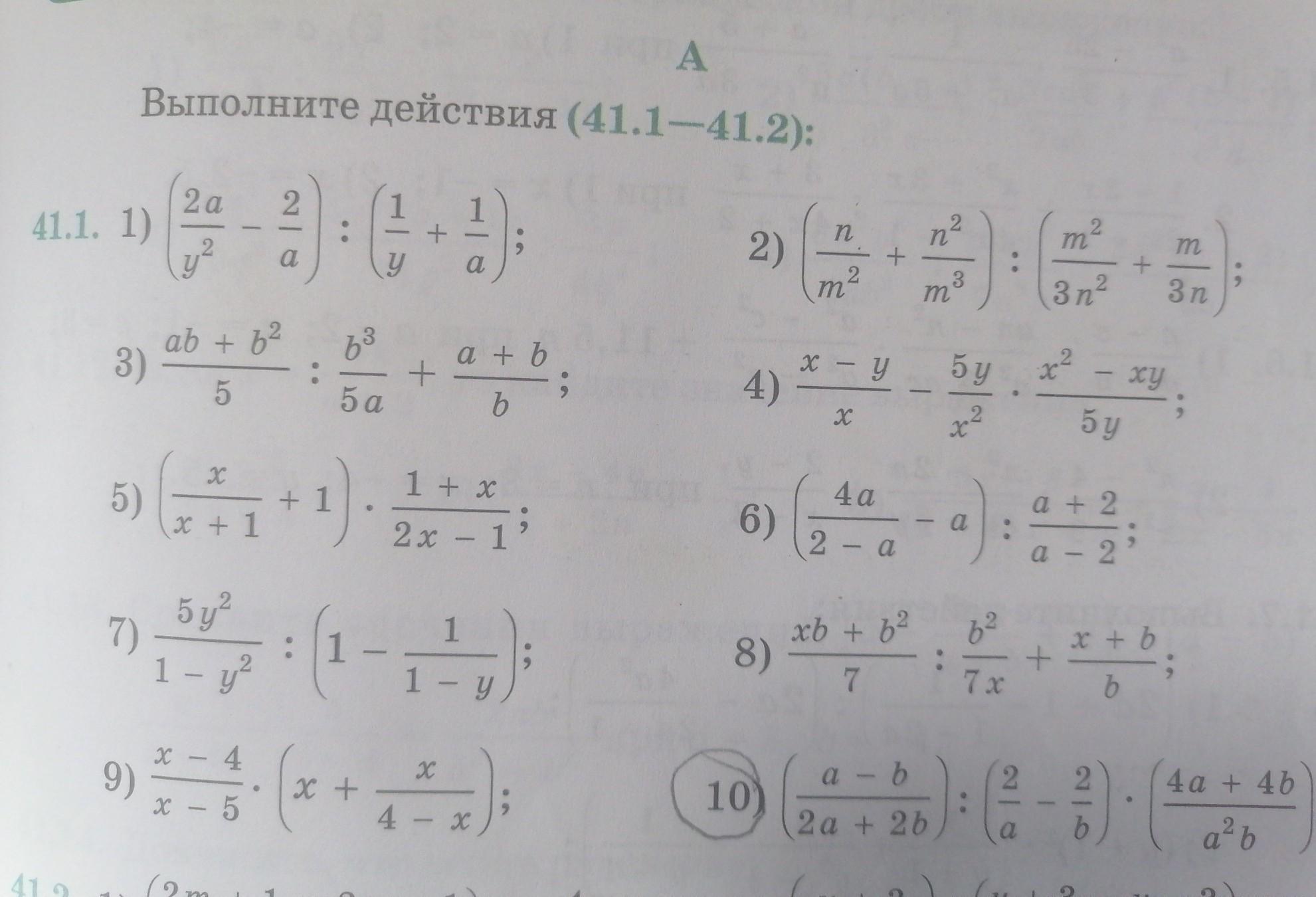10 премер полностью расписать по действиям
даю 50 баллов​

Ответ:  [tex]\frac{1}{ab-a^2}[/tex]

Объяснение:

1) первым сделаем действие во второй скобке:

[tex]\frac{2}{a} -\frac{2}{b} =\frac{2b-2a}{ab} =\frac{2(b-a)}{ab}=-\frac{2(a-b)}{ab}[/tex]

(привели к общему знаменателю и вынесли общий множитель)

2) выполним деление, предварительно вынеся общий множитель (2) в знаменателе:

[tex]\frac{a-b}{2a+2b} :(- \frac{2(a-b)}{ab}) =-\frac{a-b}{2(a+b)} : \frac{2(a-b)}{ab} =-\frac{(a-b)*ab}{2(a+b)*2(a-b)} =-\frac{ab}{4(a-b)(a+b)}[/tex]

в знаменателе пока не применяем формулу разности квадратов, так как нам надо будет сокращать в следующем действии

3) в последней скобке мы также вынесли общий множитель 4 за скобки, записали под одну черту и сократили:

[tex]-\frac{ab}{4(a-b)(a+b)}*\frac{4a+4b}{a^2b} =-\frac{ab*4(a+b)}{4(a-b)(a+b)*a^2b} =-\frac{1}{(a-b)a} =-\frac{1}{a^2-ab} =\frac{1}{ab-a^2}[/tex]